Vladimir Podolskii (NYU) - Constant-Depth Sorting Networks
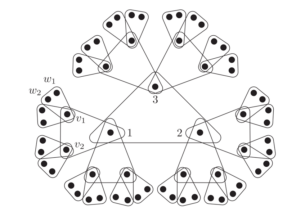
We consider sorting networks that are constructed from comparators of arity k>2. That is, in our setting the arity of the comparators — or, in other words, the number of inputs that can be sorted at the unit cost — is a parameter. We study its relationship with two other parameters — n, the number of inputs, and d, the depth. This model received considerable attention. Partly, its motivation is to better understand the structure of sorting networks. In particular, sorting networks with large arity are related to recursive constructions of ordinary sorting networks. Additionally, studies of this model have natural correspondence with a recent line of work on constructing circuits for majority functions from majority gates of lower fan-in.
We obtain the first lower bounds on the arity of constant-depth sorting networks. More precisely, we consider sorting networks of depth d up to 4, and determine the minimal k for which there is such a network with comparators of arity k. For depths d=1, 2 we observe that k=n. For d=3 we show that k=n/2. For d=4 the minimal arity becomes sublinear: k=\Theta(n^{2/3}). This contrasts with the case of majority circuits, in which k=O(n^{2/3}) is achievable already for depth d=3.
The talk is based on joint work with Natalia Dobrokhotova-Maikova and Alexander Kozachinskiy.
Speakers

Vladimir Podolskii
Vladimir Podolskii defended his PhD thesis in 2009 in Moscow State University. His research areas are computational complexity, tropical algebra, applications of complexity theory to databases augmented with logical theories. He is on leave from Steklov Mathematical Institute (Moscow) and a visiting faculty at NYU.