Timothy Black (UChicago) - Group-Theoretic Aspects of Complexity Theory and Coding Theory
Group-Theoretic Aspects of Complexity Theory and Coding Theory
Group theory has long played a role in complexity theory, and vice versa. We explore two of these connections — to evasiveness, and to local list-decoding.
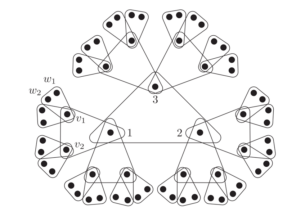
A boolean function in n variables is weakly evasive if its decision-tree complexity is Ω(n). By k-graphs we mean k-uniform hypergraphs. A k-graph property on v vertices is a boolean function on n = (v choose k) variables corresponding to the k-subsets of a v-set that is invariant under the v! permutations of the v-set (isomorphisms of k-graphs).
Rivest and Vuillemin (1976) proved that all non-constant monotone graph properties (k = 2) are weakly evasive, confirming a conjecture of Aanderaa and Rosenberg (1973). Kulkarni, Qiao, and Sun (2013) proved the analogous result for 3-graphs. We extend these results to k-graphs for every fixed k. From this, we show that monotone boolean functions invariant under the action of a large primitive group are weakly evasive.
While KQS (2013) employ the powerful topological approach of Kahn, Saks, and Sturtevant (1984) combined with heavy number theory, our argument is elementary and self-contained (modulo some basic group theory). Inspired by the outline of the KQS approach, we formalize the general framework of “orbit augmentation sequences” of sets with group actions. We show that a parameter of such sequences, called the “spacing,” is a lower bound on the decision-tree complexity for any nontrivial monotone property that is Γ-invariant for all groups Γ involved in the orbit augmentation sequence, assuming all those groups are p-groups. We develop operations on such sequences such as composition and direct product which will provide helpful machinery for our applications. We apply this general technique to k-graphs via certain liftings of k-graphs with wreath product action of p-groups.
The codewords of the homomorphism code aHom(G, H) are the affine homomorphisms between two finite groups, G and H, generalizing Hadamard codes. Following the work of Goldreich–Levin (1989), Grigorescu et al. (2006), Dinur et al. (2008), and Guo and Sudan (2014), we further expand the range of groups for which local list-decoding is possible up to mindist, the minimum distance of the code. In particular, for the first time, we do not require either G or H to be solvable. Specifically, we demonstrate a poly(1/ε) bound on the list size, i.e., on the number of codewords within distance (mindist – ε) from any received word, when G is either abelian or an alternating group, and H is an arbitrary (finite or infinite) group. We conjecture that a similar bound holds for all finite simple groups as domains; the alternating groups serve as the first test case.
The abelian vs. arbitrary result permits us to adapt previous techniques to obtain efficient local list-decoding for this case. In the alternating vs. arbitrary setting, we obtain a local algorithm that produces partial homomorphisms that uniquely extend to the homomorphisms in the list. We introduce this “semi-algorithmic” model, which we call Certificate List-Decoding, due to the severe technical difficulties in extending partial homomorphisms to full homomorphisms, even when the extension is unique. A homomorphism extender applied to a list of certificates yields the desired list.
The results on list decoding homomorphism codes are joint work with László Babai and Angela Wuu.
Timothy Black
Timothy Black is an Assistant Instructional Professor.